Quote:
Originally Posted by SamD
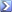
Pretty sure it's not, shifting by half a pixel right (by linear interpolation), then left again, is lossy in 1D.
|
Hi Sam,
Looks like you are right, linear interpolation is mathematically the same as a moving average of width= 2. Features get averaged out, it is strongest for smaller PSF. Hence why oversampling (beyond Nyquist) is not always a bad thing. (If we recall 2 pixels per PSF is the critical Nyquist limit which applies to bandwidth aliasing and the frequency domain...I always wondered why it was taken so literally in 2D imaging applications

)
I redid you 1D experiment in excel and graphed it for clarity, the attached chart shows the effect of two consecutive linear interpolations on 3 made up data sets (FWHM =4,3,2 pixels). The green points (first interpolation) all fall exactly on the piecewise linear curve (blue line) between data points (open blue circles) and seemingly reproduce the correct signal. However it is an illusion since shifting the points by half a pixel again (orange circles) falls off the blue line, information about the peak structure was lost, how much depends on the size of the PSF.
So just by resampling our data we are performing a small (2x2) averaging filter. Fancier algorithms such bi-cubic and Lanczos may preserve detail at smaller PSF (1.5x1.5 effective kernel?) however they have the unavoidable side effect of generating ringing artefacts (which is effectively aliasing in the frequency domain, still no free lunch !!!).
Regards,
EB